Overview

The goal of this project was to develop a path planning algorithm for a drone swarm, such that it would be able to detect emerging wildfires efficiently. This project was part of my Bachelor's Thesis Project. The main idea was that a swarm of drones equipped with cameras and other sensors would fly over a large area and continuously monitor the wildfire risk, continuously updating the paths such that the highest-risk areas are checked most often.

Technical details

The search area is divided into grid cells, where each grid cells risk will be individually measured by the drones (or estimated from external sources for the initial deployment). Then each grid cell is assigned a sector, where each sector is monitored by one drone. Each drone will then trace a pre-defined path through each sector. The reason that only one drone is allowed in each sector is to ensure that the drones do not collide with each other, even in extreme conditions (e.g. thick smoke) where communication may be lost.

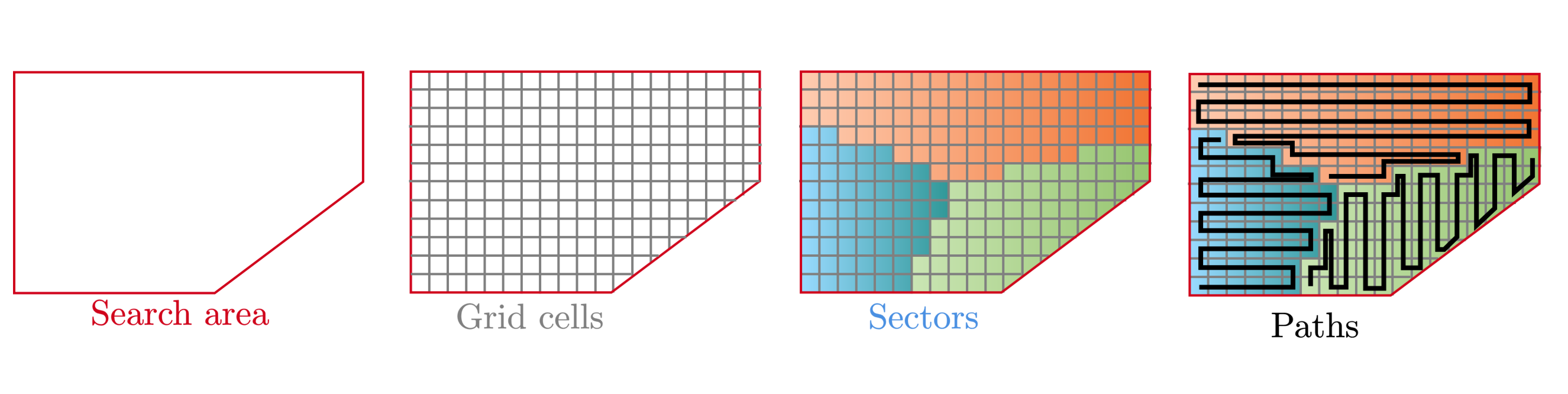
Within this framework, the main ways to optimise the monitoring are to optimise the sector divisions and to optimise the paths. I decided to limit the scope to only optimising the sector divisions. I wanted the sectors to be divided such that the aggregated risk is the most evenly distributed over the sectors. Mathematically, this meant that every cell in the search area $C_i\in \Omega$ is assigned to one of $K$ sectors $S_0, S_1, \ldots, S_K\in \mathcal{S}$ such that: $$ \begin{aligned} S_0, S_1,\ldots,S_K &= \underset{\mathcal{S}}{\text{argmin}}\left\{ \sum_{s_i\in\mathcal{S}}\left[\sum_{C_j\in s_i} R(C_j) -\frac{1}{K}\sum_{C_l\in \Omega} R(C_l) \right]^2 \right\} \\ &= \underset{\mathcal{S}}{\text{argmin}}\left\{ \sum_{s_i\in\mathcal{S}}\left(R_{s_{i}} -\overline{R}_{\Omega} \right)^2 \right\} \end{aligned} $$ Where $R: \Omega \to [0, 1]$ is the imperical risk map, $R_{s_i}$ is the cumulative risk of sector $s_i$ and $\overline{R}_\Omega$ is the average cumulative risk of the whole search area. Computationally, this condition was optimised by generating a large amount of candidate sector divisions and selecting the one that achieved the lowest value of the objective function. The candidate sector divisions were created with a Voronoi tesselation, where the generator points are sampled from the risk map using Inverse transform sampling. This has the effect of naturally reducing the sector size in high-risk areas.

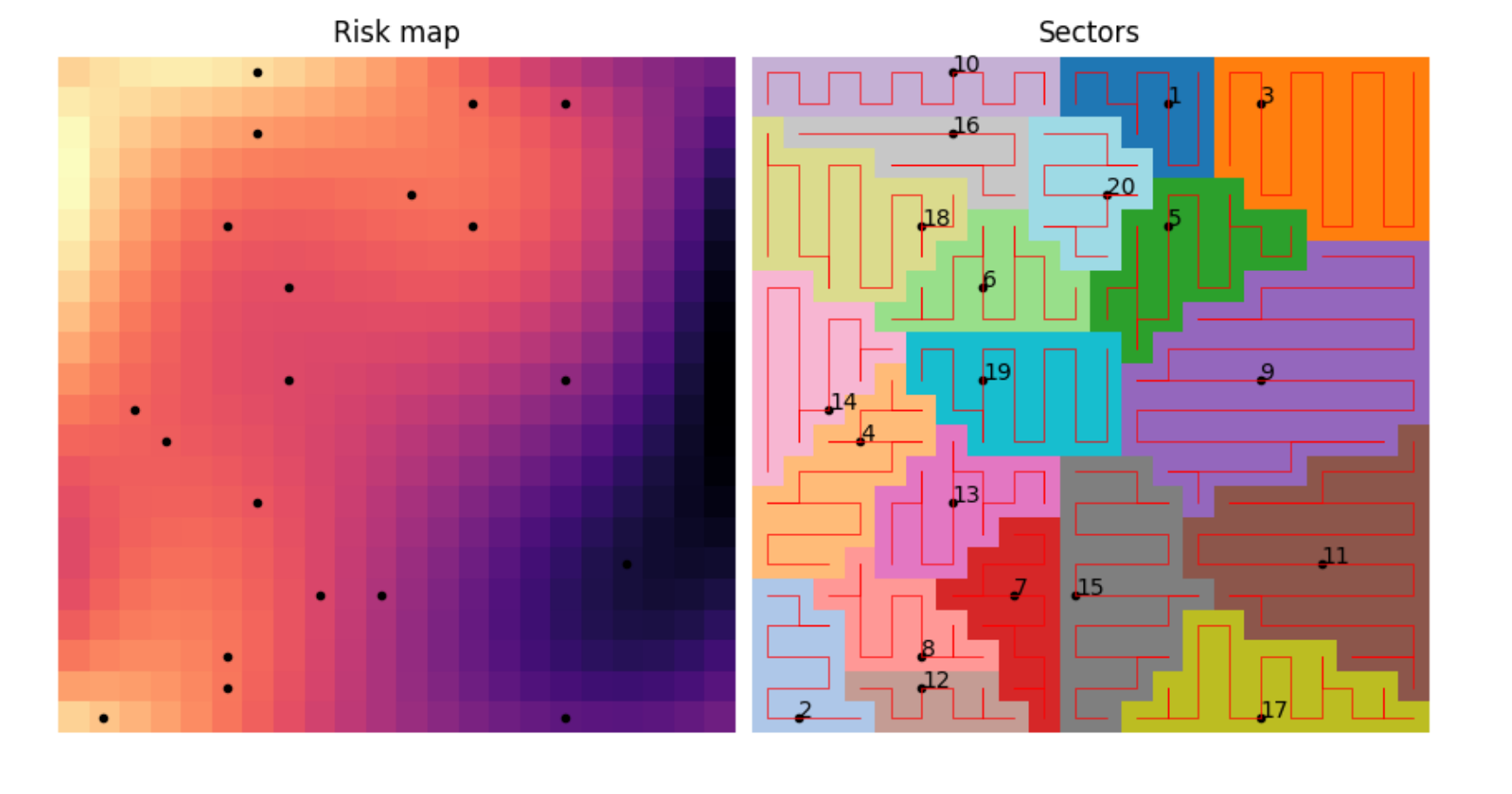
From this project I learned a lot about swarm planning, gradient-free optimisation and even graph theory. I am satisfied with the results of the project, but I am curious to explore this more. For example what would happen if the paths are also optimised, or if there is an alternative to sectors that still ensures that no drone collisions will occur.