Overview

The goal of this project was to develop a model that uses a drone's camera to estimate its distance from obstacles, to feed into a path planning algorithm. This project was part of a practical assignment for the Master course AE4317 "Autonomous Flight of Micro Air Vehicles". The core challenge was developing a depth estimation model that could work on a resource-constrained drone without any ground-truth depth data. Traditional approaches either use stereo cameras (which the drone didn't have) or supervised learning (which requires labeled depth data we didn't have access to). So we went with an unsupervised approach using a CNN to process a single camera feed.

Technical details

There are 2 main insights that underlie the unsupervised training method for a depth estimation CNN. The first is that two nearby video frames from the drone’s camera taken at known locations are related to each other by the depth map. The depth map explains the parallax between the frames (aside from possible occlusions). The second insight is that in a static environment, two nearby video frames from the drone’s camera at different points in time can be considered as two different cameras at the same point in time. With this, possible environmental changes between frames can be neglected.

To assess the accuracy of the CNN-generated depth map without ground-truth data, we used the following method. First, two nearby video frames are taken from the training set $\mathbf{I}_i$ and $\mathbf{I}_j$ at known positions $\mathbf{x}_i$ and $\mathbf{x}_j$. Then, the CNN is run on $\mathbf{I}_i$ to obtain a depth map estimate $\widehat{\mathbf{D}}_i$. Then, $\mathbf{x}_i$, $\mathbf{I}_i$ and $\widehat{\mathbf{D}}_i$ are taken to project the image into 3D-space, giving each pixel in the frame a 3D coordinate (left diagram). Then, the 3D coordinates are reprojected into the 2D focal plane at $\mathbf{x}_j$, which results in a reconstruction $\hat{\mathbf{I}}_j$. Finally, the difference between $\mathbf{I}_i$ and $\hat{\mathbf{I}}_j$ is proportional to the accuracy of $\widehat{\mathbf{D}}_i$ with respect to the (unkown) ground-truth depth map $\mathbf{D}_i$ (right diagram).

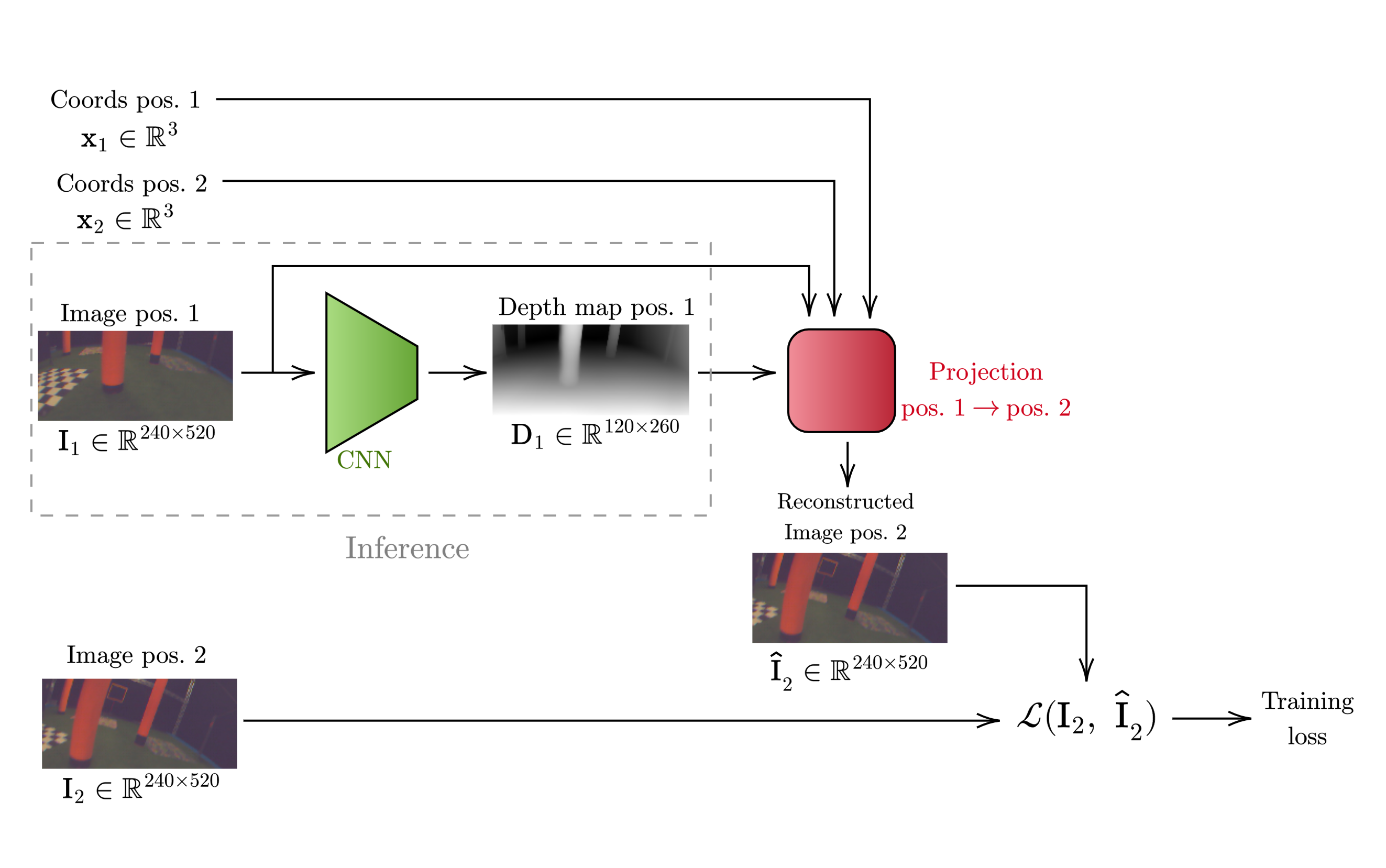
The depth reconstruction method has many advantages for our application, since it doesn't need multiple cameras or ground-truth training data, and it's very generalizable across different environments. However, we did encounter some difficulties. Firstly, the projection uses a ray-tracing algorithm, which does not provide a differentiable output. So, the training loop cannot use gradient descent to train the model, and has to use gradient-free alternatives like Simulated Annealing in our case. This makes the training process for even a small CNN very computationally intensive. Secondly, the drone’s camera uses a wide-angle lens which creates significant barrel distortions, so the pinhole-camera approximation that the projection uses is less accurate.