Overview

The goal of this project is to get a better understanding of differential geometry and quaternion transformations for 3D graphics. The project idea stemmed from a curiosity into how the range polygon of an aircraft would be affected by winds and the curvature of earth. The plan was to develop a tool where the user could move a cursor point over the surface of the earth, and a range polygon would appear over that point showing the places that the aircraft could reach from that point.

Implementation

The tool is written with the Rust programming language, using the egui framework as the front-end. This added an extra challenge because egui doesn't have a 3D pipeline, so the 3D view had to be implemented from scratch. The country border data and airport coordinates were found on Natural Earth Data. Data on global wind patterns was found in a study by Kling and Ackerly, 2020.

The range polygon generator uses a discretised ODE scheme for the Geodesic Equation with varying initial condition to estimate the range boundary. The wind is accounted for by a simple correction $ds'=ds/(1+w/V)$ where $w$ is the tailwind component and $V$ the cruise velocity.

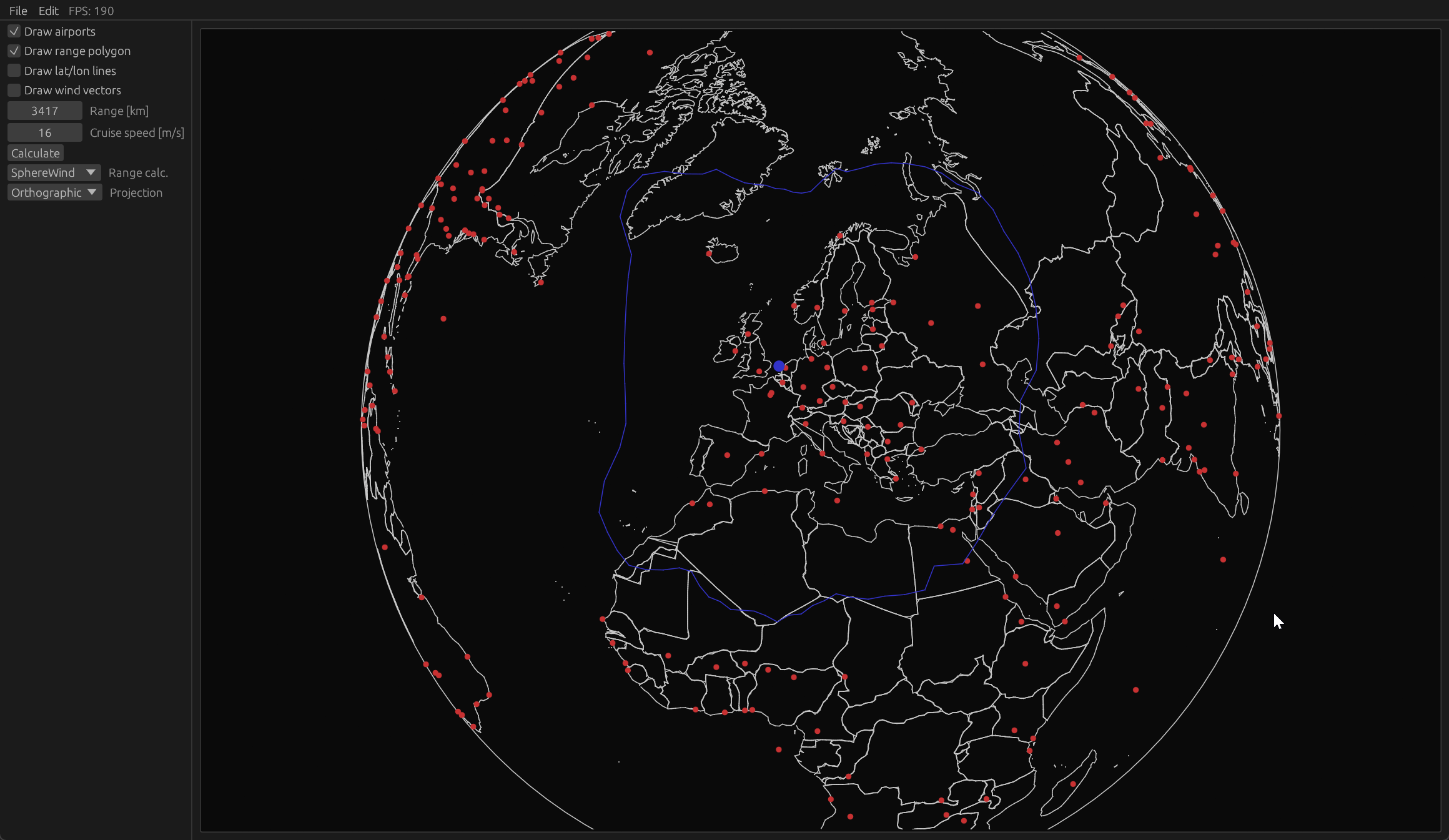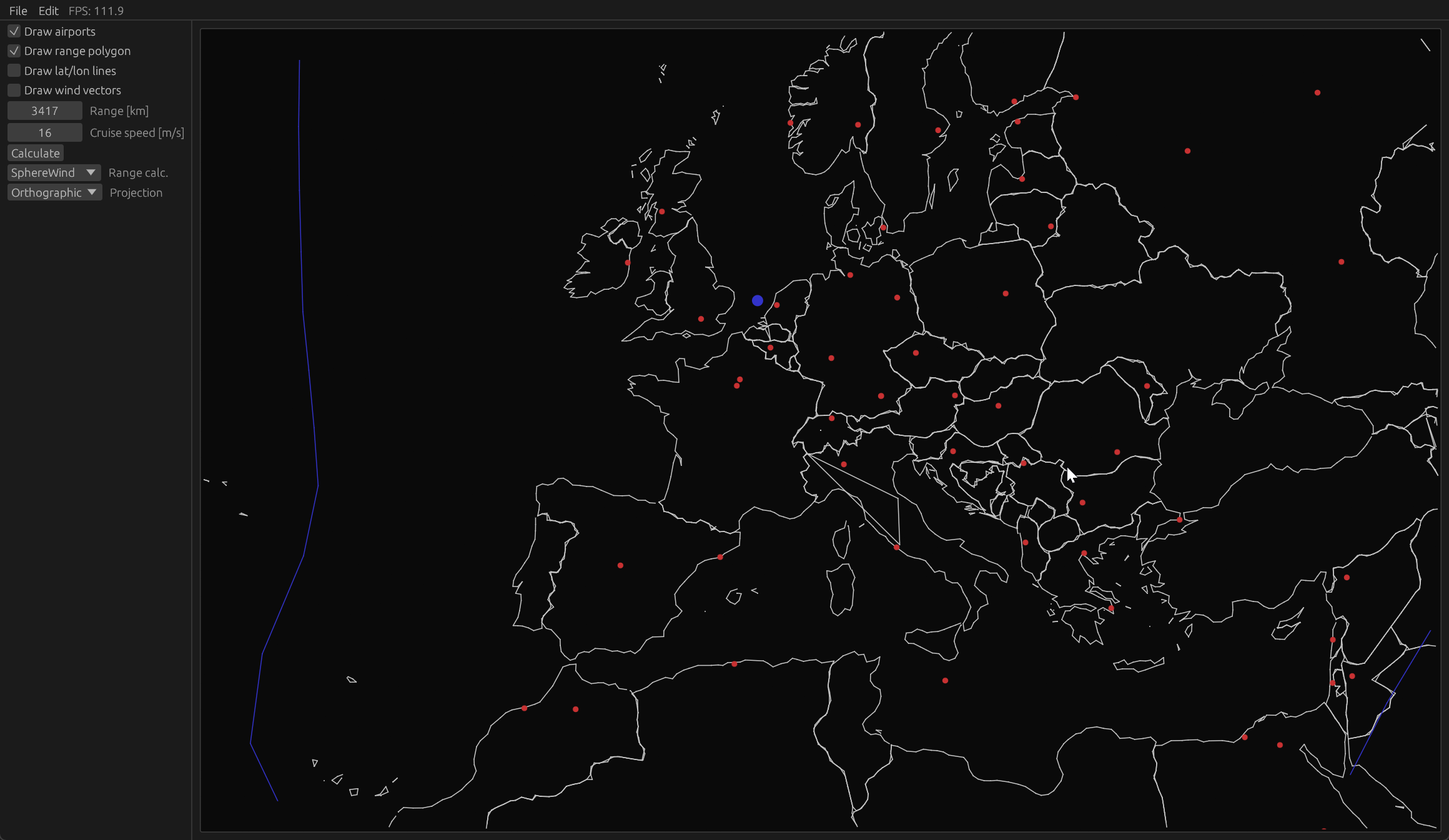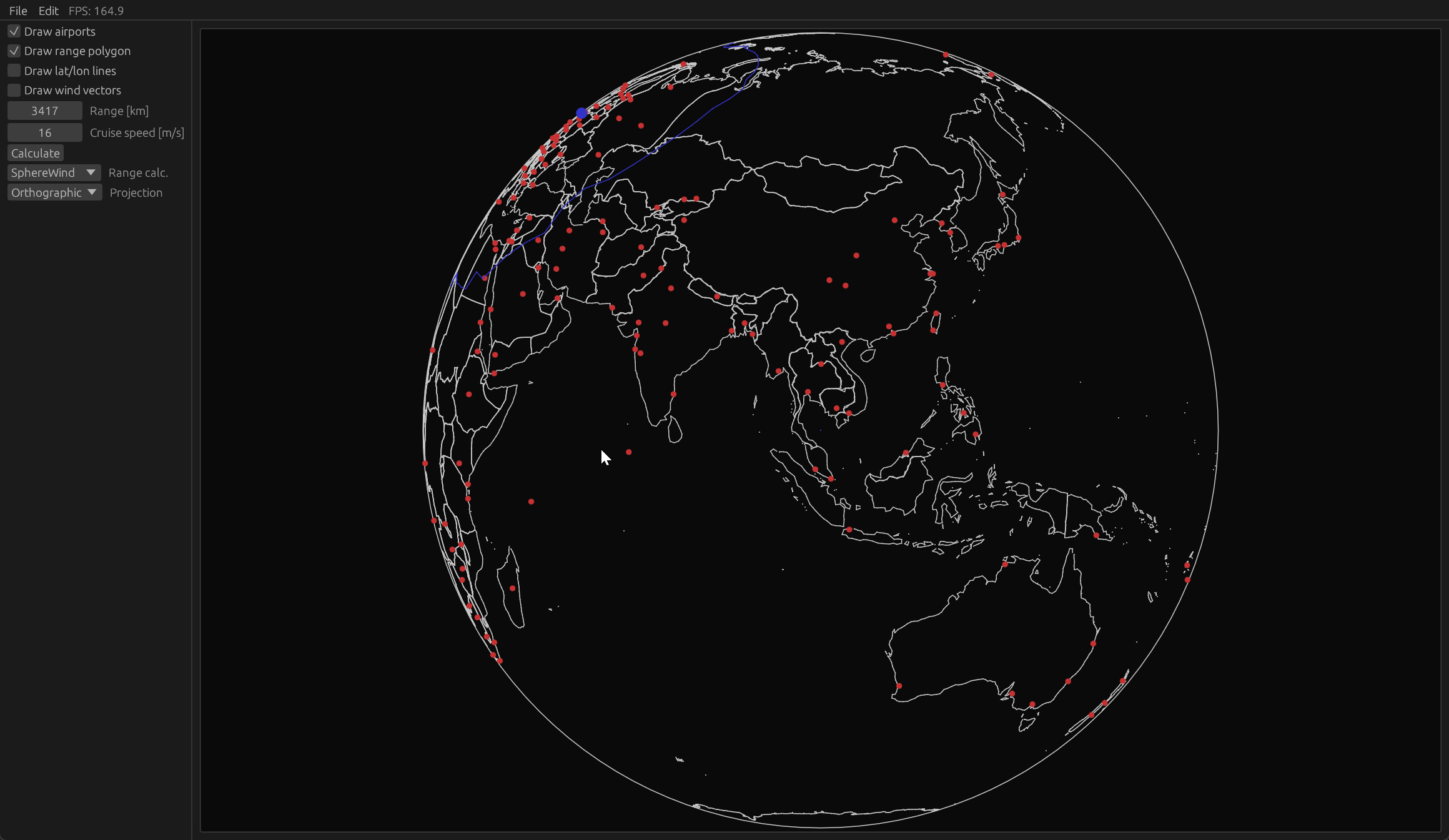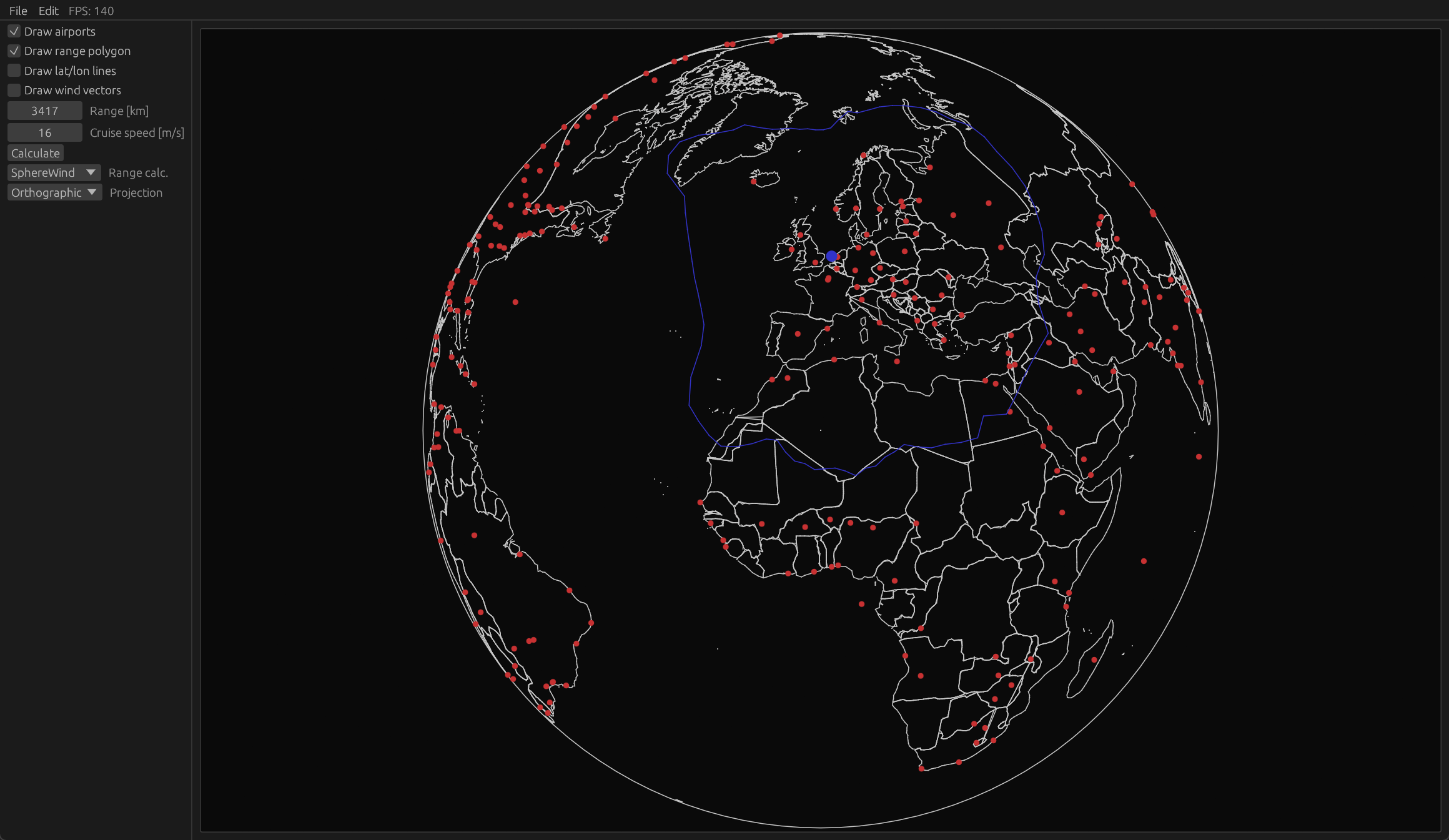
Techincal details

We define a Lat/lon-coordinate system on the unit sphere where $\theta\in[-\pi, \pi]$ and $\phi \in \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right]$: $$ \begin{aligned} x &= \cos \theta \cos \phi \\ y &= \sin \theta \cos \phi \\ z &= \sin \phi \end{aligned} $$ Tensor indices are defined as: $x^i=\{x,y,z\}$, $u^i=\{\theta, \phi\}$. Then, we expand the Geodesic Equation w.r.t. the parameters: $$ \begin{aligned} \frac{d^2 \phi}{d t^2} + \Gamma_{11}^2 \left(\frac{d\theta}{dt}\right)^2 + \Gamma_{12}^2 \frac{d\theta}{dt}\frac{d\phi}{dt} + \Gamma_{21}^2 \frac{d\phi}{dt}\frac{d\theta}{dt} + \Gamma_{11}^2 \left(\frac{d\theta}{dt}\right)^2 &= 0 \qquad (1) \\ \frac{d^2 \phi}{d t^2} + \Gamma_{11}^2 \left(\frac{d\theta}{dt}\right)^2 + \Gamma_{12}^2 \frac{d\theta}{dt}\frac{d\phi}{dt} + \Gamma_{21}^2 \frac{d\phi}{dt}\frac{d\theta}{dt} + \Gamma_{11}^2 \left(\frac{d\theta}{dt}\right)^2 &= 0 \qquad (2) \end{aligned} $$ Where $\Gamma_{ij}^k$ are the Christoffel symbols. These are defined as (using Einstein summation): $$ \Gamma^k_{ij}=\frac{1}{2}\mathfrak{g}^{kl}\left( \frac{\partial g_{li}}{ \partial u^j} + \frac{\partial g_{jl}}{ \partial u^i} - \frac{\partial g_{ij}}{ \partial u^l} \right) $$ Finding the metric tensor $g_{ij}$ and its inverse $\mathfrak{g}^{ij}$ using the Jacobian $\mathbf{J}$: $$ g =\mathbf{J}^T\mathbf{J} = \begin{bmatrix} \cos^2\phi & 0 \\ 0 & 1 \end{bmatrix} \qquad \mathfrak{g} =g^{-1} = \begin{bmatrix} \frac{1}{\cos^2\phi} & 0 \\ 0 & 1 \end{bmatrix} $$ Finding the values of the Christoffel symbols and filling them into $(1)$ and $(2)$: $$ \begin{aligned} \frac{d^2 \theta}{d t^2} - 2\tan\phi \left( \frac{d\theta}{dt}\frac{d\phi}{dt} \right) = 0 \qquad (3) \\ \frac{d^2 \phi}{d t^2} + \sin\phi\cos\phi \left( \frac{d\theta}{dt} \right)^2 = 0 \qquad (4) \end{aligned} $$ Discretising the time as $t_{i}=t_{0}+i\Delta t$, and the state as $\theta_{i}=\theta(t_{i})$ and $\phi_{i}=\phi(t_{i})$. Define $\dot{\theta}_{i}=(d\theta/dt)_{t_{i}}$ and $\dot{\phi}_{i}=(d\phi/dt)_{t_{i}}$. We have the forward Euler scheme: $$ \begin{aligned} \theta_{i+1}&=\theta_{i}+\dot{\theta}_{i}\Delta t \\ \phi_{i+1}&=\phi_{i}+\dot{\phi}_{i}\Delta t \\ \dot{\theta}_{i+1}&=\dot{\theta}_{i}+\left(d^2\theta/dt^2\right)_{t_{i}}\Delta t \\ \dot{\phi}_{i+1}&=\dot{\phi}_{i}+\left(d^2\phi/dt^2\right)_{t_{i}}\Delta t \end{aligned} $$ From Equations $(3)$ and $(4)$: $$ \begin{aligned} \left(d^2\theta/dt^2\right)_{t_{i}} &= 2\tan\phi \left( \dot{\theta}_{i}\dot{\phi}_{i} \right) \\ \left(d^2\theta/dt^2\right)_{t_{i}} &= -\dot{\theta}_{i}^2\sin(\phi_{i})\cos(\phi_{i}) \end{aligned} $$ This completes the numerical scheme. We can choose $(\theta_0, \phi_0)$ to be the origin point and vary $(\dot{\theta}_0, \dot{\phi}_0)$ to explore different directions. Then track the total distance traveled in every direction to find the range polygon.